E4. Linear logic for quantum mechanics
In the previous episodes, we saw an overview of linear logic and the various descriptions of (just the multiplicative fragment of the) logic in category theory. In this episode, how these categorical descriptions work beautifully as a language to describe quantum theory.
Traditionally, Hilbert spaces or more generally Von Neumann algebras are used as the mathematical framework of quantum mechanics. While this framework support detailed computation, they do not support an intuition for the problem: this leads to an approach described as "shut up and calculate". The programme of categorical quantum mechanics emerged out of the desire to develop an intuitive framework that aids human thinking to represent and reason about quantum processes. What is more intuitive than pictures! Categorical quantum mechanics indeed gave a pictorial way to represent quantum process, yet these pictures have precise meaning to them.
Linear logic captures the essence of quantum mechanics owing to its resource-sensitive character. We saw that in linear logic one cannot duplicate an arbitrary resource: in quantum mechanics, this is referred to as the no-cloning theorem which states that it is impossible to duplicate an arbitrary quantum state. Motivated by this connection, the field of categorical quantum mechanics uses the compact multiplicative linear logic as the base framework for its purpose, and added the notion of dagger to this fragment, thus giving rise to compact dagger-linear logic. The 'dagger' abstracts the notion of 'adjoint' which is crucial to quantum mechanics: the measurable properties of a quantum system are given by self-adjoint operators on a separable Hilbert space, that is, a Hilbert space with countable orthonormal basis.
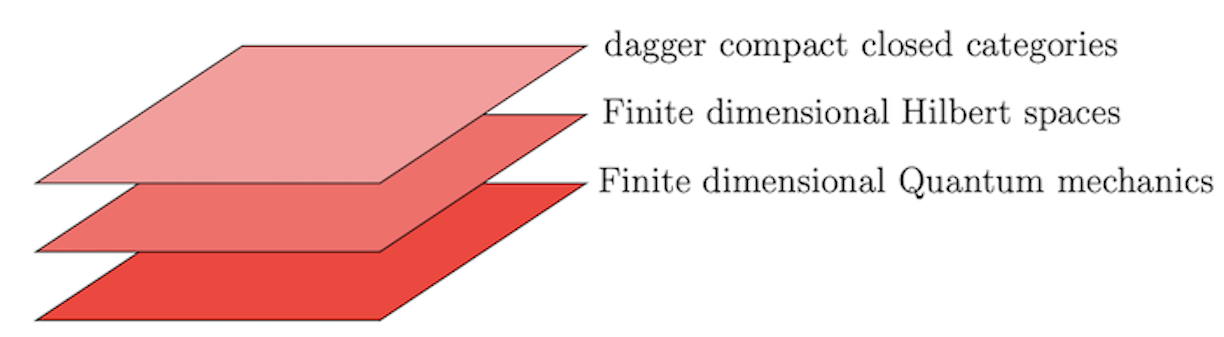
While monoidal categories provide the semantics for compact multiplicative linear logic (compact MLL), dagger monoidal categories provide the categorical semantics for compact dagger linear logic. Categorical quantum mechanics uses dagger monoidal categories, specifically, dagger compact closed categories to develop a high-level, intuitive, formal language for quantum mechanics by abstracting the standard, traditionally-used, analytical framework of Hilbert spaces, as illustrated below:
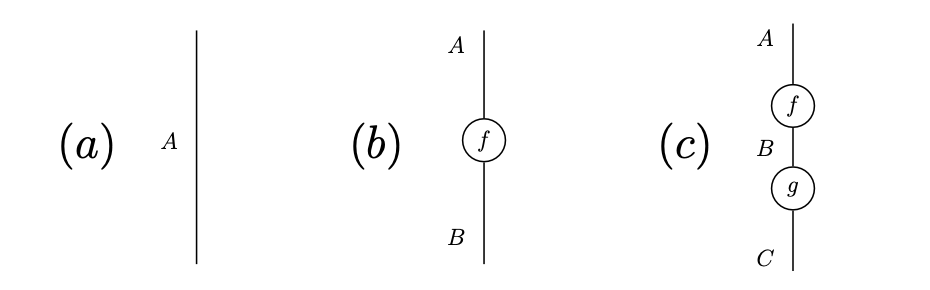
In 2004, Abramsky and Coecke [1] described the fundamental axioms of quantum mechanics within the framework of dagger compact closed categories. This was quite significant as it meant that the proof theory based on string diagrams of monoidal categories [2], could be deployed to reason about quantum processes. For example, in categorical quantum mechanics, physical systems are represented as wires and processes as circles.
The label of a wire represents its type. Diagram represents a system , and diagram represents a transformation from system to system . Processes can composed sequentially by connecting the wires with matching types. Note that the string diagrams are to be read from top to bottom (following the direction of gravity), and from left to right.
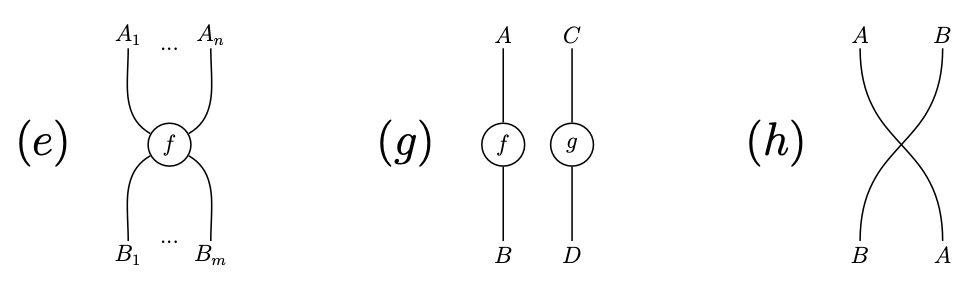
Moreover, the wires and the boxes can be composed in parallel leading to processes as shown in diagrams and . Morever, the wires are allowed to cross one another another as shown in diagram .
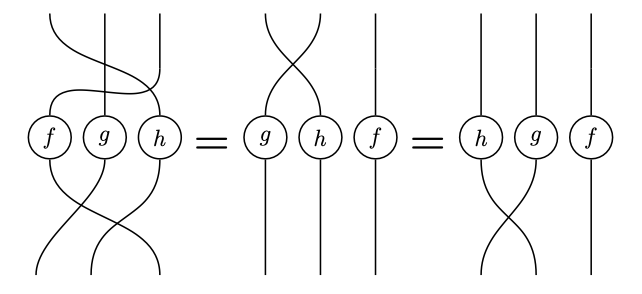
It is far simpler to reason about processes using string diagrams since the human brain is good at processing visual information. For example, it is quite easy to see that the diagrams below represent the same process: one can prove the diagrams equal by fixing the ends of the wires and moving the circles.
In compact closed categories, one can additionally bend wires into a cap and a cup as follows, thus adding to the expressive power of the language:
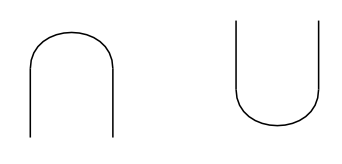
The dagger compact closed categories faithfully abstract the structure of finite-dimensional Hilbert spaces, thereby enabling a diagrammatic but rigorous reasoning technique for quantum processes within the category of finite-dimensional Hilbert spaces and linear maps.
For those of you who are interesed in learning about this pictorial approach to quantum theory, Bob and Aleks had written a book titled Picturing Quantum Processes: A First Course in Quantum Theory and Diagrammatic Reasoning which requires no prior knowledge of category theory or quantum theory!
We shall come back to quantumy stuff later in this series! Half of my thesis was about figuring an analog for dagger compact closed categories in infinite dimensions. Remember, dagger compact closed categories work only for finite-dimensional Hilbert spaces! This exploration towards infinite-dimensions is what led me to linearly distributive and star autonomous categories. More on this in the later episodes!
In the next episode, I shall introduce the star of this series, the linearly distributive categories ⭐ 🎉
References
[1]. Samson Abramsky and Bob Coecke. “A Categorical Semantics of Quantum Protocols”. In: Proceedings of the 19th Annual IEEE Symposium on Logic in Computer Science. LICS ’04. Washington, DC, USA: IEEE Computer Society, 2004, pp. 415– 425. isbn: 0-7695-2192-4.
[2]. Peter Selinger. “Dagger compact closed categories and completely positive maps”. In: Electronic Notes in Theoretical Computer Science 170 (2007), pp. 139–163.